別解っぽい面白い解き方をしたので記録に残します。
問題文
すぬけ君は黒板と$N$個の整数からなる集合$S$を持っています。$S$の$i$番目の要素は$S_i$です。
すぬけ君は黒板に整数$X$を書いたのち、以下の操作を$N$回行います。
- $S$から要素を1つ選んで取り除く。
- その後、現在黒板に書かれた数を$x$、$S$から取り除かれた整数を$y$として、黒板に書かれた数を$x \mod y$に書き換える。
$S$から要素を取り除く順序は$N!$通りありえます。 それぞれの場合について、$N$回の操作後に黒板に書かれている数を求め、その総和を$10^9+7$で割ったあまりを求めてください。
引用元: https://atcoder.jp/contests/exawizards2019/tasks/exawizards2019_d
同じ要素を選ぶことを許してみる
問題設定では$S$の要素1つごとに操作を行っていますが、これを何度でも行うことを許してみましょう。 すなわち、次の操作を好きなだけ繰り返すことを考えます。
- $S$から要素を1つ選び、$y$とする。
- 現在黒板に書かれた数を$x$として、黒板に書かれた数を$x \mod y$に書き換える。
このとき、実は2度目以降は同じ$y$を選んでも黒板に書かれた数は変わりません。 なぜなら、黒板に書かれた数は増加しない一方で、一度目の操作で$(x \mod y) < y$となるためです。
すなわち、たとえば$y$を $$ (10, 5, 8, 10, 4, 8, 8) $$ として選んだとき、これから2度目以降の$10, 8$を除いた操作 $$ (10, 5, 8, 4) $$ と最終的に同じ値となります。
ランダムに無限回操作してみる
さて、上記の操作をランダムに無限回繰り返すことを考えてみましょう。 すなわち、次の操作を無限回繰り返すことを考えます。
- $S$からランダムに要素を1つ選び、$y$とする。
- 現在黒板に書かれた数を$x$として、黒板に書かれた数を$x \mod y$に書き換える。
このとき、確率$1$で要素$S$のすべてを少なくとも1回ずつ選びます。 「要素$S$のすべてを少なくとも1回ずつ選ぶ操作」を考えてみます。 そのような操作では、上述のように2度目以降の要素を除くことで、$S$の要素$N$個を1度ずつ選ぶ操作に対応します。 そしてその並び順は、ランダムに選んだことから任意の並び方について$1 / N!$の確率で選ばれます。
以上の議論により、次の値が同じであることがわかります。
- $S$からランダムに要素を1つずつ取り除くとき、最終的に黒板に書かれた数が$n$である確率。
- 無限回$S$からランダムに要素を選ぶとき、最終的に黒板に書かれた数が$n$である確率。
(最終的に$n$である確率は、「$i$回ランダムに操作したあとに$n$である確率」の$i \rightarrow \infty$における極限値とします)
また、前者の確率が求まったとき、期待値を計算し$N!$倍することで出力値となります。 したがって、後者を効率的に計算できれば十分です。
ランダムに無限回操作したとき最終的に$n$である確率
現在黒板に$x$が書かれているとします。 $y \in S$が選ばれた場合、黒板の数は$x$から$x \mod y$へ遷移します。
黒板にかかれている数を頂点として、遷移を有向辺で貼ってみます。 黒板に書かれた数は増加しないため、DAGに自己ループを生やしたものとなります。
次の画像は$X = 8, S = \{3, 5\}$の場合のグラフです。 紫色の辺が$5$、オレンジ色が$3$を選ぶ遷移です。
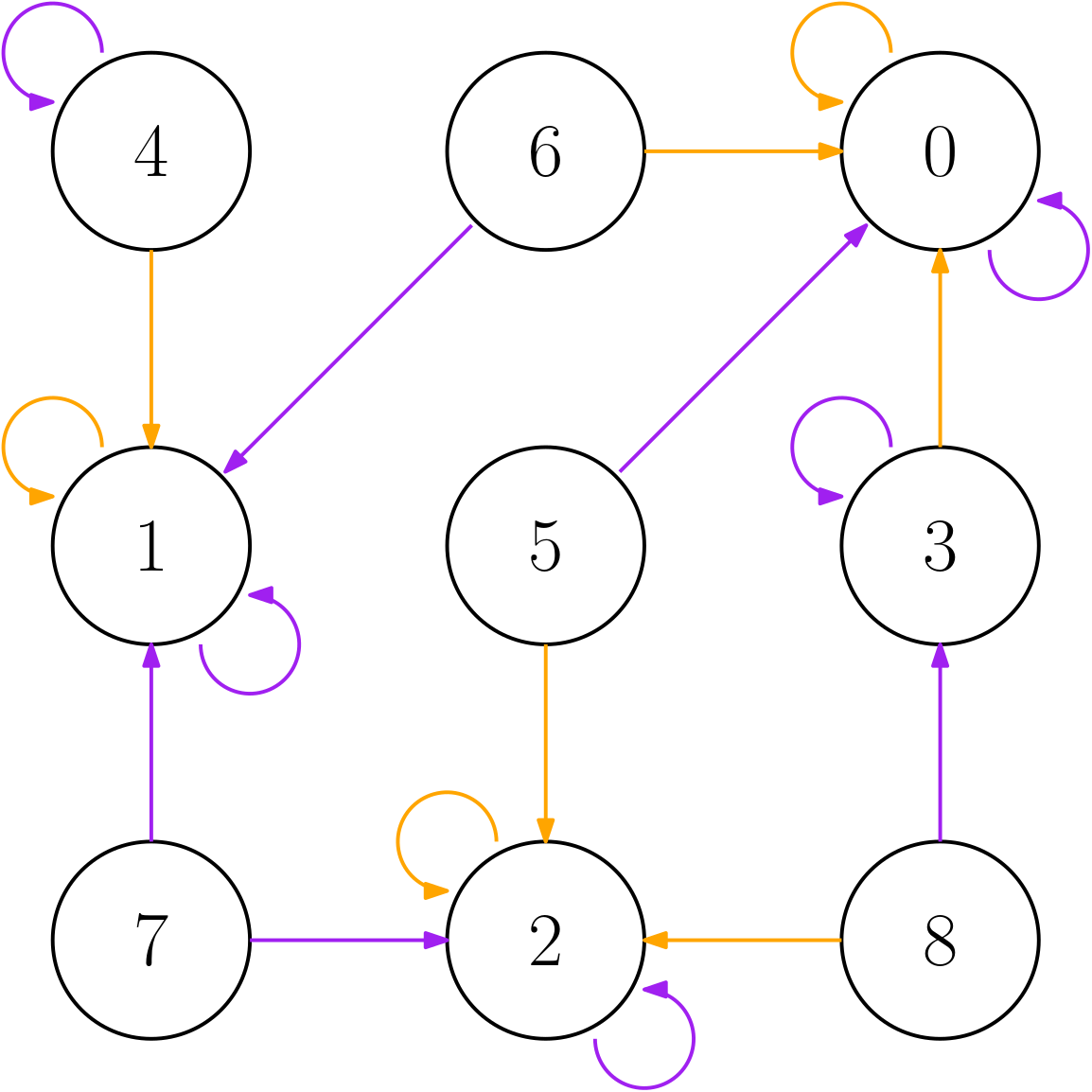
ランダムに無限回操作したとき、最終的に$n$である確率を考えます。 天下り的に書くと、これは$X$から確率$1$をDAG上で等しく分配していくことで計算できます。
具体的には、次の計算をこれをトポロジカルソート順に$X$からやっていきます。 はじめ$X$は確率$1$を持っているとします。
頂点$n$から、頂点$m_1, m_2, \dots, m_k \ (n \neq m_i)$へ辺が貼られているとします。 このとき、$m_1, m_2, \dots, m_k$へ、頂点$n$の持っている確率$p(n)$を$p(n) / k$ずつ分配します。 そして頂点$n$の持っている確率を$0$とします。
最終的に得られる$p(n)$が、欲しい確率となります。
気持ちとしては、「$X$からはじめて、$i$回操作後に$n$にいる確率」$p_i(n)$を、漸化式で考えるとわかります。 上記の画像の例から一部頂点を抜粋して書くと、
$$ p_{i+1}(3) = \frac{1}{2} ( p_{i}(8) + p_{i}(3)), $$ $$ p_{i+1}(0) = p_{i}(0) + \frac{1}{2} (p_{i}(3) + p_{i}(5) + p_{i}(6)), $$
となります。 グラフがDAG + 自己ループの形をしているため、最終的には頂点$0$のような「他頂点へ辺が向かっていない頂点」へ確率が溜まっていくわけです。 それを計算しています。
さいごに
以上を用いて、atcoder::modint1000000007 で以下を計算して出力します。
$$ N! \cdot \sum_{x \in \{0, 1, \dots, X\}} x \cdot p(x). $$
計算量は$O(NX)$で想定解と同じです。